1 Introduction

In recent years, there has been a notable increase in the utilization of mobile robots in a variety of fields, including the military and industry, for the performance of essential unmanned tasks (Deguale et al., 2024). As the complexity of use scenarios and the level of safety standards continue to evolve, the challenge of efficiently and accurately planning driving paths has become a significant research topic (Meng et al., 2023). The planning of robot paths has consistently been a topic of significant interest within the field of robotics. It enhances the autonomy and operational efficiency of robots in diverse environments, offering substantial benefits for applications across various sectors of modern society (Kong et al., 2024). The fundamental objective of path planning is to identify the optimal route from the initial position to the intended destination of the robot, which typically necessitates a comprehensive assessment of factors such as distance, time, energy consumption, and the safety of the path (Guo et al., 2020). An optimal path should be free of obstacles, minimize detours, and facilitate efficient navigation (Junli et al., 2020). Mobile robots frequently operate in environments with diverse obstacles and unknown variables, underscoring the importance of path planning algorithms that can effectively avoid obstacles and operate in real-time with high reliability (Sha et al., 2023).

The existing body of literature on path planning algorithms can be divided into two main categories: traditional algorithms and those based on machine learning (Yuwan et al., 2022). The traditional path planning algorithms include Ant Colony Optimization (Lei et al., 2023), A* algorithm (Yu et al., 2024), Particle Swarm Optimization (Meetu et al., 2022), Dijkstra algorithm (Zhou et al., 2023), Genetic Algorithm (Debnath et al., 2024), Dynamic Window Approach (Chuanbo et al., 2023), and Artificial Potential Field algorithm (Zhang et al., 2023), among others. While these algorithms are widely used, they also have corresponding shortcomings, including low planning efficiency, poor search ability, and the tendency to fall into local optima. In recent years, the application of Deep Reinforcement Learning (DRL) algorithms in the field of path planning has been significantly advanced by the progress of hardware technology. DRL integrates the robust feature extraction capabilities of Deep Learning (DL) with the decision optimization abilities of Reinforcement Learning (RL), thereby offering a novel approach to address the limitations of traditional path planning algorithms (Chen et al., 2024). The DRL algorithm most widely used in path planning is the Deep Q Network (DQN) algorithm proposed by the DeepMind team (Lin and Wen, 2023). The DQN effectively addresses the “curse of dimensionality” problem faced by Q-value tables in complex environments by utilizing a neural network to replace the Q-value table in the Q-Learning algorithm. However, the traditional DQN algorithm exhibits shortcomings such as overestimation of Q-values and slow network convergence.

In light of the shortcomings of the DQN algorithm, Huiyan et al. (2023) put forth an augmented DDQN (double DQN) approach to path planning, which enhances the efficacy of algorithmic training and the precision of optimal path generation. Jinduo et al. (2022) put forth a double DQN-state splitting Q network (DDQNSSQN) algorithm that integrates state splitting with optimal states. This method employs a multi-dimensional state classification and storage system, coupled with targeted training to obtain optimal path information. Yan et al. (2023) put forth an end-to-end local path planner n-step dueling double DQN with reward-based ϵ-greedy (RND3QN) based on a deep reinforcement learning framework, which acquires environmental data from LiDAR as input and uses a neural network to fit Q-values to output the corresponding discrete actions. The problem of unstable mobile robot action selection due to sparse rewards is effectively solved. Shen and Zhao (2023) put forth a DDQN-based path planning framework for UAVs to traverse unknown terrain, which effectively mitigates the issue of overestimation of Q values. Wang et al. (2024) put forth an extended double deep Q network (DDQN) model that incorporates a radio prediction network to generate a UAV trajectory and anticipate the accumulated reward value resulting from action selection. This approach enhances the network’s learning efficiency. In a further development of the field, Li and Geng (2023) proposed a probabilistic state exploration ERDDQN algorithm. This has the effect of reducing the number of times the robot enters a repeated state during training, thus allowing it to explore new states more effectively, improve the speed of network convergence, and optimize the path planning effect. Tang et al. (2024) put forth a competitive architecture dueling-deep Q network (D3QN) for UAV path planning, which further optimizes the calculation of Q value and facilitates more precise updates to network parameters. Yuan et al. (2023) proposed the D3QN-PER path planning algorithm, which employs the Prioritized Experience Replay (PER) mechanism to enhance the utilization rate of crucial samples and accelerate the convergence of the neural network.

The aforementioned research has enhanced the functionality of the DQN algorithm to a certain degree; nevertheless, there are still significant issues that require attention, including low sample utilization, slow network convergence, and unstable reward convergence. To address this issue, this paper proposes a BiLSTM-D3QN path planning algorithm based on the DDQN algorithm. First, a BILSTM network is introduced to render the neural network memory-based, thereby increasing the stability of decision-making and thus facilitating more stable reward convergence. Secondly, a competitive network is introduced to further address the issue of overestimation of the neural network’s Q-value, thereby enabling the network to update more rapidly. The proposal of adaptive reprioritization of experience replay based on frequency penalty function is intended to facilitate the extraction of crucial and recent data from the experience pool, thus accelerating the convergence of the neural network. Finally, an adaptive action selection mechanism is introduced with the objective of further optimizing action exploration.

2 Related work 2.1 Q-Learning algorithm

Reinforcement Learning is an important branch of machine learning that aims to learn how to take the best action in a given situation by interacting with the environment in order to maximize cumulative rewards. Reinforcement learning differs from supervised learning and unsupervised learning in that it emphasizes trial and error in interacting with the environment for feedback, constantly adjusting strategies to achieve the best results. The basic framework of reinforcement learning is shown in Figure 1. The agent chooses action at based on current state st. The environment provides reward rt for the current action and state st+1 for the next moment based on the action. After continuous interaction, the agent’s decision is improved and updated to obtain a higher reward rt.

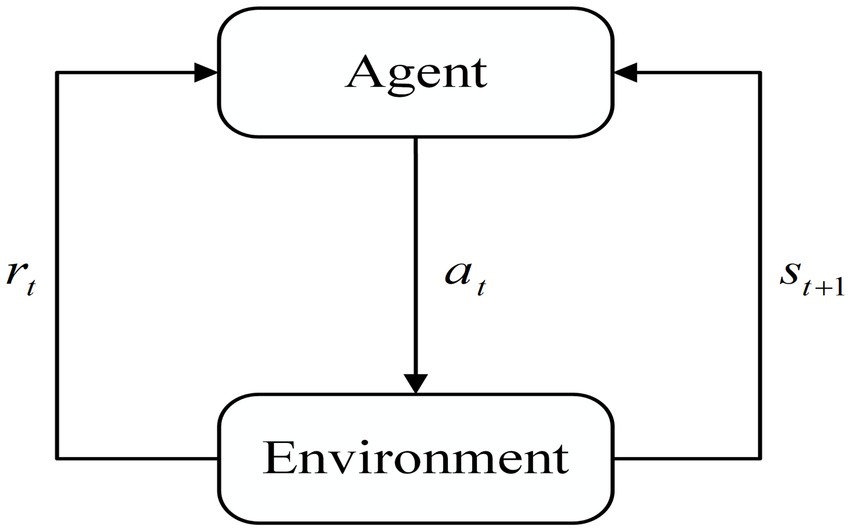
Figure 1. Basic reinforcement learning architecture.

The Q-Learning algorithm is a model-free reinforcement learning method based on a value function. It selects the optimal strategy by updating the action value function Q. The update of Q value is shown in Equation 1:

Qstat←Qstat+αrt+γmaxa′Qst+1a′−Qstat    (1)

Where Qstat denotes the Q-value of the intelligent body for selecting action at in the current state st; α denotes the learning rate; γ denotes the discount factor; rt denotes the reward value obtained after executing action at, and maxa′Qst+1a′ denotes the maximum Q-value for the next state.

2.2 DQN algorithm

The traditional DQN algorithm, as proposed by the DeepMind team, is based on the Q-Learning algorithm. The introduction of a neural network as the carrier of the value function allows for the nonlinear approximation of the state value function through the use of a neural network with parameters ω and an activation function. This approach enhances the efficiency of path planning. In contrast to the Q-Learning algorithm Q-value table, the DQN employs a neural network to address the dimensional explosion problem that arises in complex environments (Chen et al., 2024). However, the conventional DQN approach selects the action with the maximum Q-value when searching for the optimal action, which is susceptible to overestimation of the Q-value during network updates. Figure 2 illustrates the structure of the DQN algorithm.

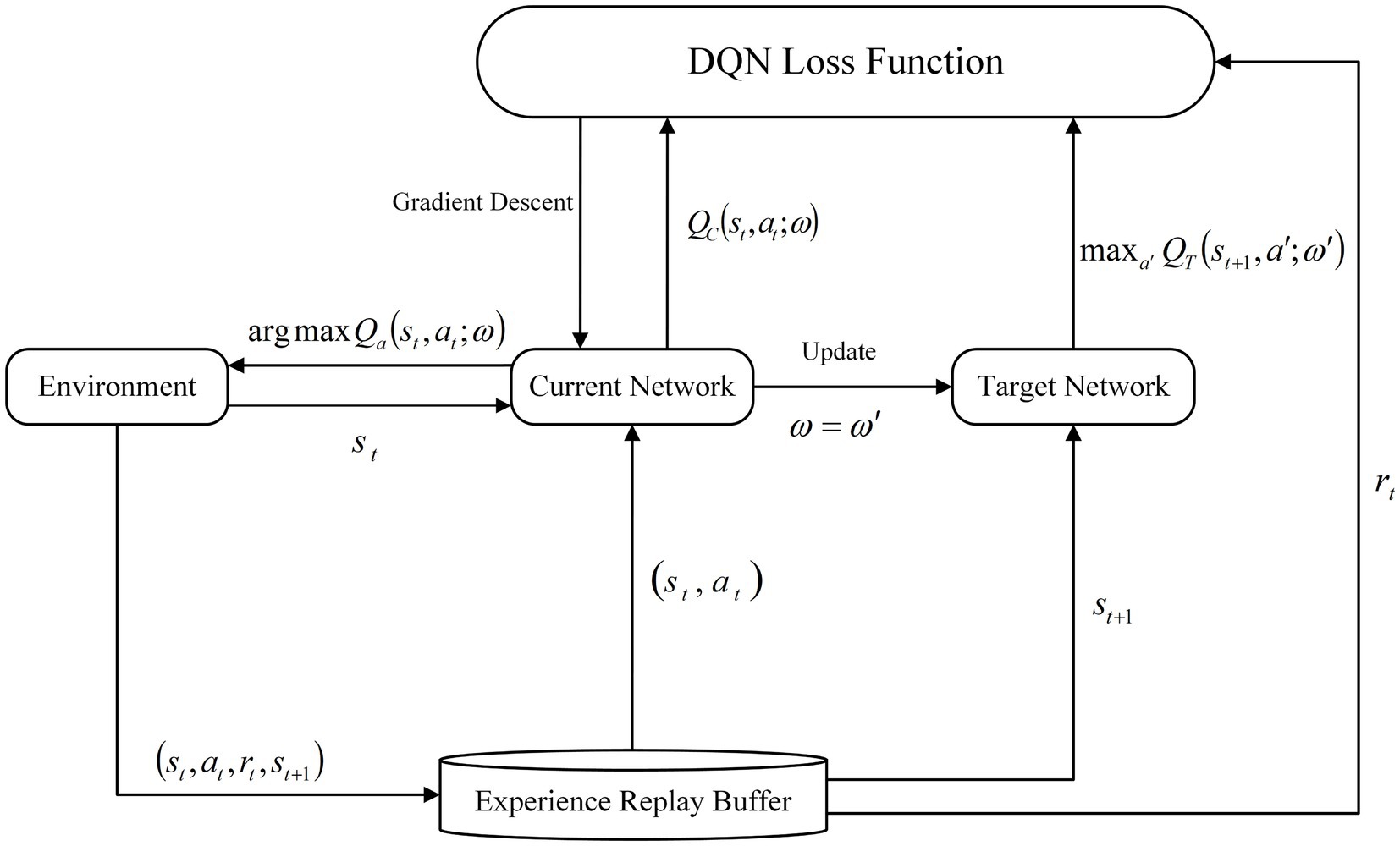
Figure 2. Schematic diagram of DQN structure.

The DQN neural network comprises two networks with identical structures: the current network (QC) and the target network (QT). The algorithm employs the current network to calculate an estimated value for a given state and utilizes the output value of the target network in conjunction with a sequential difference method to perform gradient descent, thereby updating the current network. Once the current network has undergone a specified number of updates, the target network is updated by copying the parameters C of the current network. During the training phase, a random and uniform sample is selected from the experience replay pool and provided to the two neural networks for the purpose of gradient descent with respect to the loss function. The calculation formula is presented in Equations 2,3.

LLoss=QCstatω−Qtarget2    (2) Qtarget=rt+γmaxa′QTst+1a′ω′    (3)

Where ω is the current network parameter and ω′ is the target network parameter; γ is the discount factor; QCstatω is the current network output value; and maxa′QTst+1a′ω′ is the maximum action value of the target network at state st+1.

Following the calculation of the loss value, the DQN updates the network parameter ω through the application of the gradient descent method. The gradient descent formula is presented in Equation 4.

ωt+1=ωt+EQtarget−QCstatωt∇QCstatωt    (4) 2.3 DDQN algorithm

In response to the issue of overestimation of the Q value in the DQN algorithm, the DeepMind team put forth the DDQN algorithm as a potential solution. In comparison to the DQN algorithm, the DDQN algorithm modifies the manner in which the Q value is calculated within the target network. This involves the decomposition of the maximization operation within the target network into the utilization of distinct networks for the purposes of action selection and action evaluation. In contrast to the conventional approach of selecting the maximum Q value, the DDQN algorithm initially identifies the action a′ that corresponds to the maximum Q value in state st+1 through the current network. The target network then calculates the Q value based on action a′ and the current state st+1. This process effectively mitigates the issue of overestimation of Q values (Yuan et al., 2023), leading to more precise Q value estimation. The structural diagram of the DDQN network is illustrated in Figure 3.

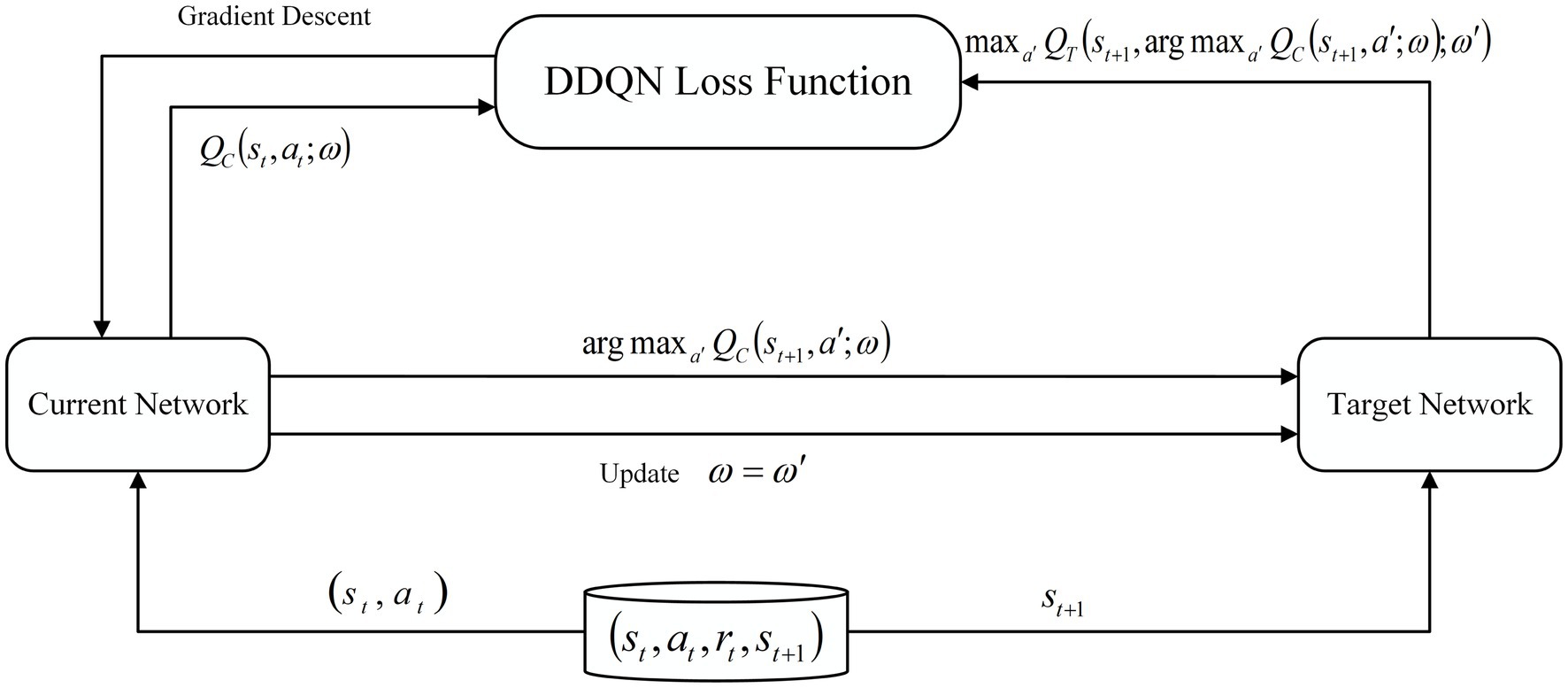
Figure 3. Schematic diagram of DDQN structure.

The Target Value in the DDQN algorithm is calculated as shown in Equation 5:

Qtarget=rt+1+γQTst+1,argmaxa′QCst+1a′ω;ω′    (5)

where a′ represents the set of all possible actions in the next state st+1; and argmaxa′QCst+1a′ω represents the action with the largest Q value selected by the current Q network in st+1.

3 BiLSTM-D3QN path planning algorithm

While DDQN addresses the issue of overestimation of Q-values to a degree, it nevertheless exhibits certain shortcomings and constraints. In the DDQN algorithm, the value of ε is a constant. In the latter stages of path planning, the robot may fail to identify the optimal path due to the random selection of actions. While the experience replay buffer addresses the issue of data correlation, it also presents a challenge in efficiently sampling representative experiences from the experience pool to accelerate network convergence. Furthermore, when the robot encounters the same obstacle, it may execute disparate actions, which impedes the value function from attaining convergence. This ultimately results in an unstable decision-making process. In light of these considerations, this paper puts forth a BiLSTM-D3QN path planning algorithm founded upon the DDQN decision-making model.

3.1 Design of reward function

In the context of mobile robot path planning, the term “state” is defined as the position coordinates of the robot, as illustrated in Equation 6:

Its action space is shown in Figure 4.

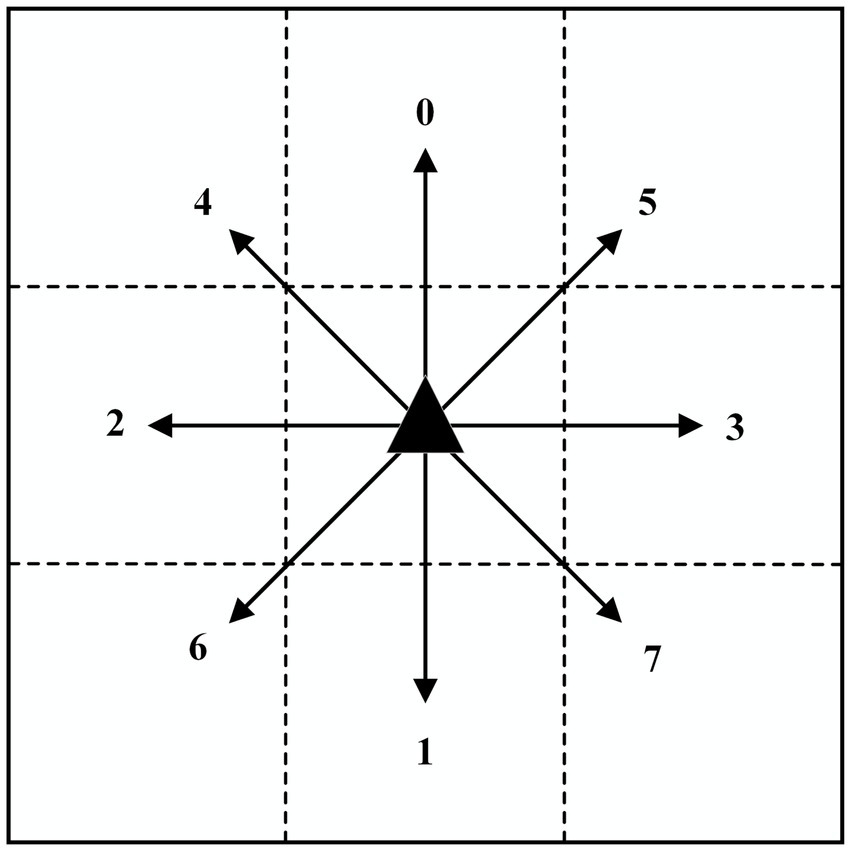
Figure 4. Schematic diagram of the action space.

The area in which the robot is permitted to move is divided into a grid, and the robot is therefore able to move freely to any of the eight surrounding grids. The digits 0 through 7 are used to represent the eight directions: front, back, left, right, top left, top right, bottom left, and bottom right, respectively. The action set is illustrated in Equation 7:

Reward functions are a key component of research in the field of RL on path planning. Classical DRL algorithms typically employ sparse reward functions, as discussed in Zhao et al. (2024). The classical DRL algorithm is designed with arrival rewards and collision rewards, with a positive reward of 20 given for arrival at the target point and-20 for collision, and the reward function is shown in Equation 8:

rt={20reachgoal−20collision    (8)

Since only the arrival and collision rewards are set during the training process, it results in a sparse reward signal. When the mobile robot acts, ineffective actions often occur. In general, terms, when the robot completes the action, if the reward value is 0 at this time, the robot can not judge what to do next based on the current state, and it is not clear how to reach the target position. Due to the difficulty of pre-exploration, the robot needs to go through a longer trial-and-error process to find the correct path. During this process, the robot is mainly guided by the negative rewards from collisions and lacks the guidance of positive rewards, so it is difficult to update a better strategy during strategy evaluation.

One solution to the reward sparsity problem is to add auxiliary rewards, and in this paper, we introduce a dynamic reward function. Distance and direction rewards are added to the environment as auxiliary rewards, and the reward values are dynamically presented with the change of robot position. The closer the mobile robot is to the target point, the greater the reward is. The reward function is shown in Equation 9:

rt={20reachgoaljΔl3other−2a∈A0123−2.5a∈A4567−5outofstep−20collision    (9)

To ensure safety in the path planning process, the simulation environment is given to the obstacle expansion. When the distance between robot and the obstacle is less than 0.1 m it is considered to have collision, and the distance between the robot and the target point is less than 0.1 m it is considered to have reached the target point, and the distance between the mobile robot and the target point is calculated as shown in Equation 10:

Δl=xcurrent−xgoal2+ycurrent−ygoal2    (10)

where Δl is the Euclidean distance between the robot and the target position at time t; j is the distance-assisted reward constant, which is used to adjust the scale of the reward; xcurrentycurrent is the current position of the mobile robot and xgoalygoal is the target point position.

The improved dynamic reward function in this paper is shown in Equation 11:

In the gradient update of the neural network value function, the error term is shown in Equation 12:

δt=Qtarget−QCstatωt    (12)

When the reward rt is sparse, the change of δt is drastic and has high variance, which affects the convergence. By introducing a smooth reward function, the variance of the gradient update term and the gradient update formula are shown in Equations 13 and 14:

Varδt=VarQtarget+VarQCstatωt    (13) ∇ωLLossω=EQtarget−QCstatωt∇QCstatωt    (14)

Sparse rewards can lead to the following problems:

1. The target value Qtarget is discontinuous: when the rewards are sparse, rt is zero in most time steps, resulting in an unsmooth change in the value of Qtarget;

2. Invalid gradient: When rt is mostly zero, the update signal (Qtarget−QCstatωt) of the gradient becomes sparse and has high variance, leading to difficulty in optimization. By introducing a smooth reward function with continuous non-zero values, the problem of sparse reward where most of rt is zero is eliminated. The continuity of rt makes the distribution of the objective value Qtarget more continuous, which directly reduces the variance of Qtarget. Convergence is improved.

The visualization of the signal distribution for the traditional and dynamic reward functions is shown in Figure 5. Assuming that the target point location of the mobile robot is (0.50, 0.50), the highlighted reward peaks at 20 when the Euclidean distance Δl between the robot and the target location is a minimum value of 0.1. The traditional reward function reward signal on the left side is only activated in a small area (with a radius of about 0.1) of the target point, and the other regions are almost unrewarded. The reward signal is very sparse, leading to inefficient training of the reinforcement learning algorithm. The right dynamic reward function reward signal gradually increases as the distance between the mobile robot and the target point decreases, and the color gradually changes from bright (high reward value) to dark (low reward value), forming a smooth gradient field. The dynamic reward function can alleviate the sparse reward problem by extending the reward coverage and establishing a gradient reward field, thus significantly improving the algorithm’s performance. This gradient reward design can effectively guide the mobile robot towards the target direction.

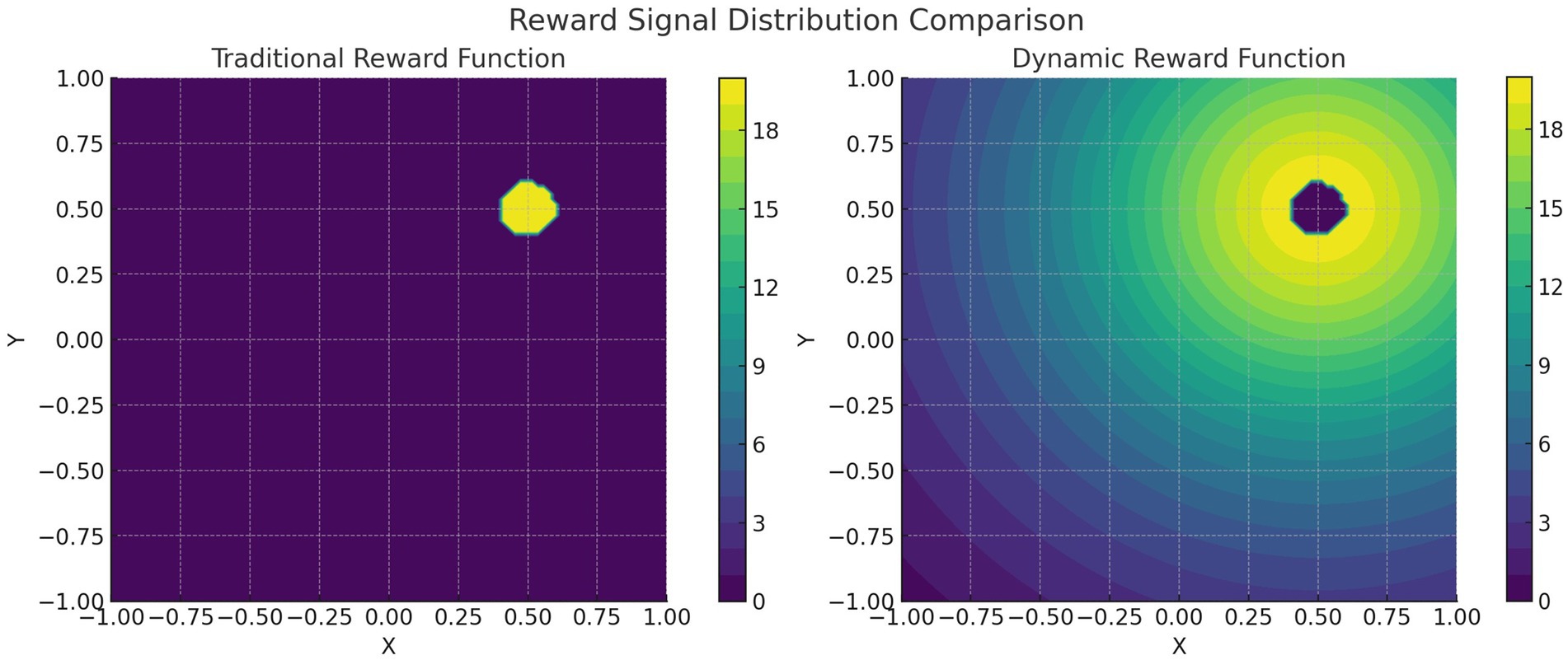
Figure 5. Visualization of signal distributions with traditional and dynamic reward functions.

3.2 Adaptive action selection mechanism

In the traditional action selection strategy, ε in the ε-greedy strategy is a fixed value. First, this may lead to insufficient exploration in the early stage of the system, which is easy to fall into the local optimal solution and unable to find the global optimal solution. In addition, there is too much exploration in the later stage, which can lead to slower convergence and the inability to effectively utilize the currently learned optimal policy, affecting the final performance. To avoid falling into a local optimum, the ε-greedy policy is improved so that the value of ε is no longer a fixed value and decreases linearly as planning progresses. The action selection mechanism in the early stage of planning selects actions more randomly by probability, and in the later stage it is more likely to select actions with large reward values. The action selection function is shown in Equation 15:

at=argmaxaQstaωn>εrandomAn≤ε    (15)

where n is a random number between 0 and 1; the exploration factor ε represents the degree of random exploration of the environment; and the set of all actions is denoted A.

At each time step t, the selection of action at is divided into two cases:

1. When n is greater than ε, the action a that maximizes Qst,;a,;ω in the current state st is selected. This means that in this case the algorithm prefers to select the action with the highest reward in the current estimation, i.e., it utilizes the best-known action.

2. When n is less than ε, choose a random action from the set of all possible actions A. This means that in this case, the algorithm prefers to randomly explore new actions to discover potentially better strategies.

ε dynamic adjustment is shown in Equation 16:

εt=εmin+εmax−εmin⋅1−tT    (16)

where t is the current number of cycles; T is the total number of cycles; εmax is the maximum exploration rate; and εmin is the minimum exploration rate.

To achieve a smooth transition of ε, the most commonly used method is linear decay. As the number of cycles of t increases, the value of 1−tT gradually decreases, and the exploration rate ε gradually decreases from the maximum value εmax to the minimum value εmin. When t is equal to 0, εt is equal to εmax, which means that in the initial stage, the exploration factor is at the maximum value, and the algorithm prefers random exploration. When t is greater than 0 and less than T, the exploration factor gradually finds a balance between exploration and utilization. When t is equal to T, εt is equal to εmin, which means that in the final stage, the exploration factor is at its minimum value and the algorithm prefers to utilize the best-known action. This satisfies the exploration degree in the early stage and avoids missing the optimal path in the later stage, while retaining the possibility of randomly selecting actions with lower probability.

3.3 Adaptive reprioritization of experience replay based on frequency penalty function

In traditional DQN algorithms, experience playback is usually done by sampling uniformly from the experience pool, which is less efficient. Therefore, academics have proposed a prioritized experience replay (PER) based on temporal difference error (TD Error), where experiences with large TD Error usually indicate higher learning value. However, there are places where PER can be optimized. In this paper, we propose adaptive reprioritization of experience replay based on frequency penalty function, whose core concept is to reflect the change in importance of experience by combining the TD Error and the frequency with which the experience is used. The frequency-of-use-based penalty function reduces the probability of being sampled again by dynamically adjusting the priority of those experiences that have been sampled multiple times. The penalization function using the frequency and the prioritization of experience are shown in Equations 17 and 18:

pi=δi+ρν⋅fui    (18)

where pi is the priority of data i; δi is the TD Error; the parameter ρ is set to avoid pi being 0; ν is a parameter controlling the degree of amplification of the priority; fui is the penalization function using the frequency; ui is the number of times the experience i has been sampled; and μ is the penalty rate constant.

The probability of each piece of data being drawn is shown in Equation 19:

where the denominator is the sum of all data priorities; k is the number of data in the experience pool.

The preference for playing back experiences with high TD error leads to the problem that the neural network training process is prone to oscillations or even divergence. Therefore the importance of sampling weight ωi is introduced to solve this problem. As shown in Equation 20:

ωi=1N⋅1Piβ    (20)

where N is the number of data in the experience pool; parameter β controls the influence of importance sampling weights in the learning process.

3.4 Dueling Network

This paper introduces a competitive network into the neural network structure of the DDQN algorithm. The competitive network introduces a dual layer with two branches between the hidden layer and the output layer of the DDQN network, which are, respectively, the advantage function layer A and the state value function layer V. The advantage function layer calculates the advantage of each action relative to the average, and the state function layer calculates the state value of the object in its current state. The advantage value of each action is summed with the state value to obtain the Q-value of each action. The problem of overestimation of the Q-value by the neural network can be further solved. The structure of the competition network is shown in Figure 6.

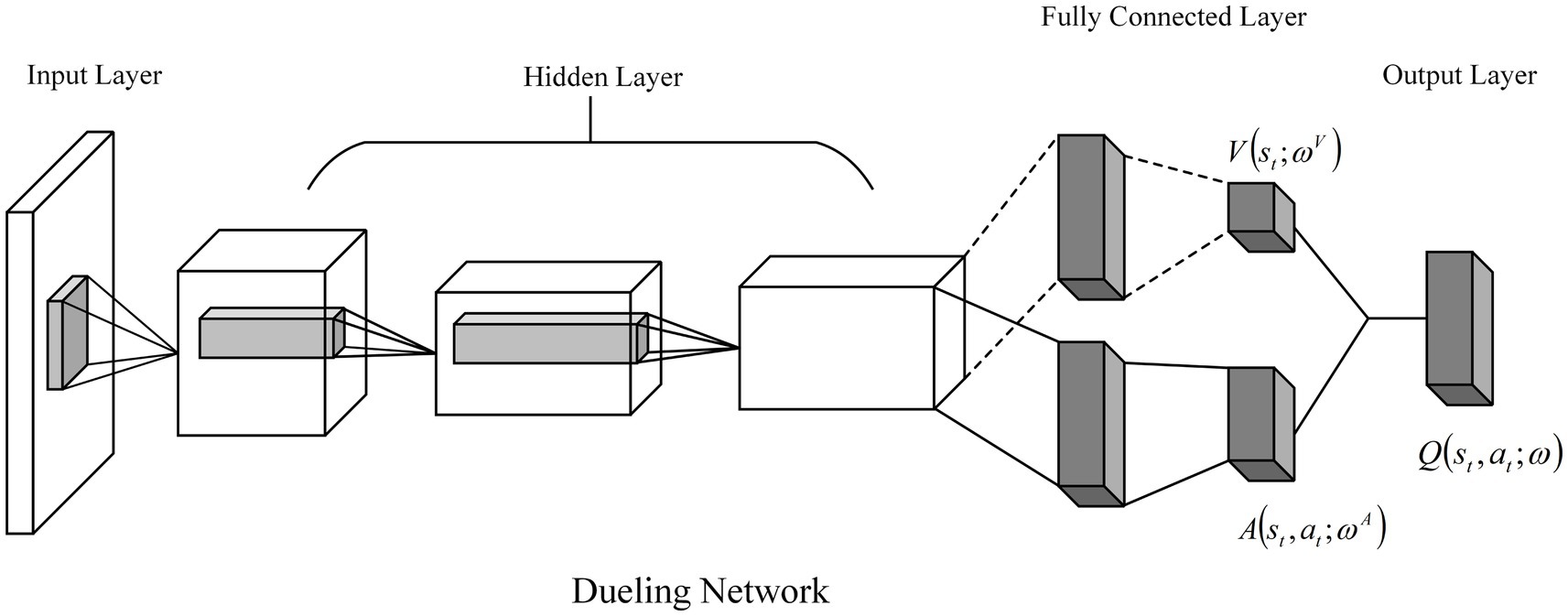
Figure 6. Schematic diagram of the Dueling Network architecture.

The Q value calculation for the Dueling DQN is shown in Equation 21:

Qstatω=AstatωA+VstωV−1A∑a′Asta′ωA    (21)

where AstatωA is the dominant value function in state st; VstωV is the state value function in state st; ωA and ωV are the network parameters of the dominant and state value functions, respectively; |A| is the size of the action space; and ∑a′Asta′ωA is the average of all action values obtained from the dominant value function layer.

This is precisely because in a competitive network, the Q value of network Q is calculated by summing up the Value Function and the Advantage Function. The existence of the Value Function allows the Algorithmic Network to evaluate the state value that is not affected by actions, thereby improving the accuracy of the Q value calculation and the algorithm’s efficiency.

3.5 Bidirectional long short-term memory network

In this paper, a Bidirectional Long Short-Term Memory Network (BiLSTM) is introduced to solve the problem of poor decision-making due to partial observability based on the DDQN decision model. By adding BiLSTM, the action selection is correlated before and after. The decision-making is more stable when facing the same obstacle, and the reward converges more stably in path planning.

3.5.1 Long short-term memory network

Long Short-Term Memory (LSTM) is an improvement of Recurrent Neural Network (RNN), which solves the problem of “vanishing gradient” in model training by adding memory units. The basic units of the LSTM network include forgetting gates, input gates, and output gates. Therefore, LSTM can effectively retain and update long-term memory and process complex time series data. The network structure is shown in Figure 7.

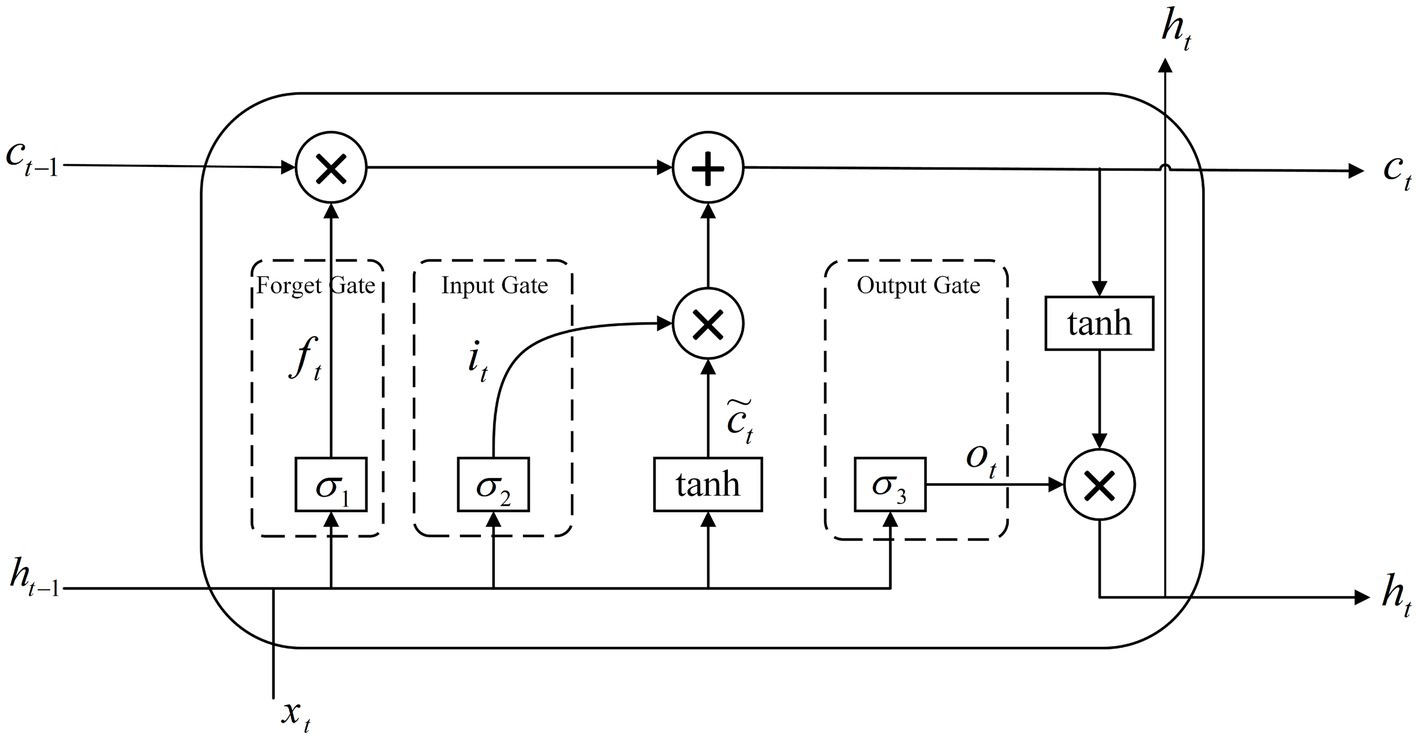
Figure 7. Schematic diagram of the LSTM structure.

ft is the output of the forgetting gate at the moment t; it is the output of the input gate at the moment t; ot is the output of the output gate at the moment t; ct is the cellular state of the memory cell LSTM at the current moment; ct−1 is the cellular state of the memory cell LSTM at the previous moment; xt is the input vector at the current moment; ht is the output vector at the current moment; σ is the activation function; and ht−1 is the output at the previous moment.

The core of LSTM is the forgetting gate, which is responsible for preserving long-term memory and is used to decide the data to be preserved in the historical information and to select the memorized information for the Sigmoid nonlinear transformation. Its formula is shown in Equation 22:

ft=σWxfxt+Whfht−1+bf    (22)

where Wxf and Whf are the weight parameters of the forgetting gate; bf is the bias parameter of the forgetting gate.

The input gate is used to control the size of the data flowing into the memory cell, and the information in the memory cell can be updated using Equation 23 and Equation 24:

it=σWxixt+Whiht−1+bi    (23) C˜t=tanhWCxt+WCht−1+bC    (24)

where Wxi and Whi are the weight matrices of the input gates; bi is the bias vector of the input gates; C˜t is the temporary variable used to compute ct; WC is the neural network parameter; and bC is the deviation vector.

The effect of the previous moment memory cell on the current moment memory cell can be expressed by Equation 25:

ct=ft⊙ct−1+it⊙C˜t    (25)

where ⊙ stands for the Hadamard product operation.

The output gate is used to determine the output value of the LSTM network and the current input features and the previous moment output are passed to the activation function to compute the output at the current moment. The computational formula is shown in Equation 26 and Equation 27:

ht=ot⊙tanhct    (26)